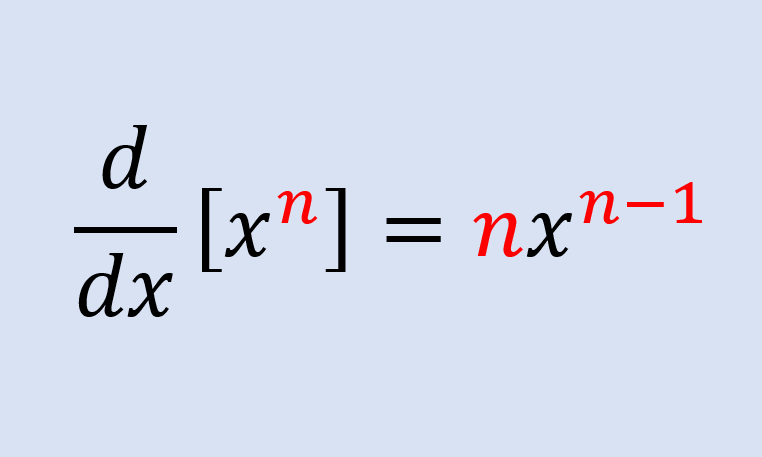✅ Para calcular fácilmente la derivada de x al cuadrado, usa la regla de potencia: baja el exponente y réstale uno, obteniendo 2x.
Calcular la derivada de x al cuadrado es un proceso sencillo y fundamental en el cálculo diferencial. La derivada de una función describe la tasa de cambio de la función con respecto a una variable independiente. En este caso, la derivada de x2 con respecto a x se puede obtener aplicando las reglas básicas de la derivación.
A continuación, vamos a detallar paso a paso cómo se puede calcular la derivada de x2 de manera fácil, utilizando la regla de la potencia.
Paso 1: Conocer la Regla de la Potencia
La Regla de la Potencia en cálculo diferencial establece que si tienes una función de la forma f(x) = xn, donde n es cualquier número real, la derivada de f(x) con respecto a x es:
f'(x) = n * xn-1
Paso 2: Identificar la Función
En este caso, nuestra función es:
f(x) = x2
Aquí, n = 2.
Paso 3: Aplicar la Regla de la Potencia
Usando la regla de la potencia, sustituimos n por 2 en la fórmula mencionada:
f'(x) = 2 * x2-1
Esto simplifica a:
f'(x) = 2 * x1
Paso 4: Simplificar la Expresión
Finalmente, simplificamos la expresión para obtener la derivada de x2:
f'(x) = 2x
Ejemplo Práctico
Supongamos que deseamos encontrar la derivada de la función f(x) = x2 en el punto x = 3. Aplicando la derivada que hemos calculado:
f'(3) = 2 * 3 = 6
Por lo tanto, la derivada de x2 es 2x. Este resultado nos indica que la tasa de cambio de x2 con respecto a x es el doble del valor de x en cualquier punto dado. Esta técnica puede aplicarse a cualquier función polinómica utilizando la regla de la potencia.
Paso a paso para derivar x al cuadrado
Derivar una función puede parecer una tarea complicada al principio, pero con los pasos correctos, se puede hacer de manera sencilla y rápida. Aquí te mostramos cómo derivar x2 de forma simple.
1. Identifica la función original
La función que vamos a derivar es x2. Esta es una función polinómica donde el exponente es 2.
2. Aplica la regla del poder
Para derivar xn, usamos la regla del poder, que se expresa como:
d/dx (xn) = nxn-1
En este caso, n es igual a 2.
3. Sustituye el valor de n en la regla del poder
Aplicando la regla del poder a nuestra función x2, tenemos:
d/dx (x2) = 2x2-1
Esto simplifica a:
d/dx (x2) = 2x
4. Verifica tu resultado
Es importante verificar nuestro resultado para asegurarnos de que es correcto. En este caso, la derivada de x2 es 2x. Esto se puede comprobar fácilmente mediante la definición de la derivada como el límite:
f'(x) = limh→0 [f(x+h) – f(x)] / h
Aplicando esto a x2:
- f(x) = x2
- f(x+h) = (x+h)2
- f(x+h) – f(x) = x2 + 2xh + h2 – x2
- (f(x+h) – f(x)) / h = (2xh + h2) / h = 2x + h
- limh→0 (2x + h) = 2x
Ejemplo práctico
Supongamos que tenemos una función que modela la posición de un objeto en movimiento, s(t) = t2, donde t es el tiempo en segundos. La derivada de esta función nos dará la velocidad del objeto en cualquier momento t:
s'(t) = 2t
Así, si queremos saber la velocidad en el segundo 3, simplemente sustituimos t = 3 en la derivada:
s'(3) = 2(3) = 6 m/s.
Consejos prácticos
- Practica derivando diferentes funciones polinómicas para familiarizarte con la regla del poder.
- Usa software de cálculo o aplicaciones móviles para verificar tus resultados al principio.
- Recuerda que la derivada nos da la tasa de cambio de una función respecto a su variable independiente.
Con estos pasos y consejos, derivar x2 será una tarea sencilla y rápida. ¡Continúa practicando y pronto derivarás funciones más complejas con facilidad!
Ejemplos prácticos de derivadas de funciones cuadráticas
Para comprender mejor cómo calcular la derivada de una función cuadrática, vamos a revisar algunos ejemplos concretos. Estas funciones son fundamentales en el cálculo y tienen múltiples aplicaciones en campos como la física, la economía y la ingeniería.
Ejemplo 1: Derivada de f(x) = x²
El primer paso es aplicar la regla básica de la derivación para potencias. Recordemos que para una función de la forma f(x) = x^n, su derivada es f'(x) = n * x^(n-1).
- Función original: f(x) = x²
- Aplicar la regla: f'(x) = 2 * x^(2-1)
- Entonces, la derivada es: f'(x) = 2x
Esto significa que la pendiente de la curva en cualquier punto x es el doble del valor de x en ese punto. Por ejemplo, en x = 3, la pendiente sería 2 * 3 = 6.
Ejemplo 2: Derivada de f(x) = 3x² + 2x + 1
Ahora consideremos una función cuadrática más compleja. Para derivarla, aplicamos la regla de la suma, que nos permite derivar cada término por separado.
- Función original: f(x) = 3x² + 2x + 1
- Derivar cada término:
- (3x²)’ = 3 * 2x = 6x
- (2x)’ = 2
- (1)’ = 0
- Sumar las derivadas: f'(x) = 6x + 2
En este caso, la derivada f'(x) = 6x + 2 nos indica que la pendiente de la curva varía linealmente con x. Por ejemplo, en x = 1, la pendiente sería 6 * 1 + 2 = 8.
Consejos Prácticos
- Memoriza las reglas básicas: La regla de la potencia y la regla de la suma son esenciales para derivar funciones cuadráticas.
- Practica con diferentes funciones: Cuanto más practiques, más fácil será identificar patrones y aplicar las reglas adecuadamente.
- Verifica tus resultados: Utiliza software de cálculo simbólico para verificar tus derivadas y asegurarte de que son correctas.
Aplicaciones en el Mundo Real
Las derivadas de funciones cuadráticas tienen numerosas aplicaciones en el mundo real. Por ejemplo, en física, la derivada de la posición con respecto al tiempo nos da la velocidad de un objeto. En economía, la derivada de una función de coste puede ayudarnos a encontrar el punto óptimo de producción.
| Campo | Aplicación de Derivadas Cuadráticas |
|---|---|
| Física | Velocidad y aceleración de objetos en movimiento |
| Economía | Optimización de costos y beneficios |
| Ingeniería | Análisis de tensiones y deformaciones en estructuras |
Preguntas frecuentes
¿Qué es una derivada?
Una derivada es la tasa de cambio instantánea de una función en un punto dado.
¿Cómo se calcula la derivada de una función cuadrática?
Para derivar una función cuadrática, se aplica la regla de la potencia: se baja el exponente y se multiplica por el coeficiente.
¿Qué es la regla de la potencia en cálculo diferencial?
La regla de la potencia establece que al derivar una función potencial, se baja el exponente y se multiplica por el coeficiente.
- La derivada de una constante es cero.
- La derivada de x a la potencia n es n*x^(n-1).
- La derivada de una suma es la suma de las derivadas.
- La derivada de un producto es el primer término por la derivada del segundo más el segundo término por la derivada del primero.
- La derivada de un cociente es la resta de las derivadas dividida por el segundo término al cuadrado.
¡Déjanos tus comentarios y visita otros artículos de nuestra web sobre cálculo y matemáticas que pueden ser de tu interés!