✅ Para calcular la raíz cuadrada de b al cuadrado, simplemente toma el valor absoluto de b: √(b²) = |b|. ¡Matemáticas simples y directas!
Para calcular la raíz cuadrada de b al cuadrado, simplemente debes conocer que la raíz cuadrada y la potencia son operaciones inversas. De manera directa, la raíz cuadrada de b al cuadrado es el valor absoluto de b, denotado matemáticamente como √(b²) = |b|. Esto se debe a que elevar un número al cuadrado y luego sacar la raíz cuadrada de ese resultado te devuelve el valor inicial, pero en su forma no negativa.
Ahora bien, vamos a desglosar este proceso y explicar detalladamente cómo funciona la operación de la raíz cuadrada y la potenciación, así como algunos ejemplos prácticos para una mejor comprensión.
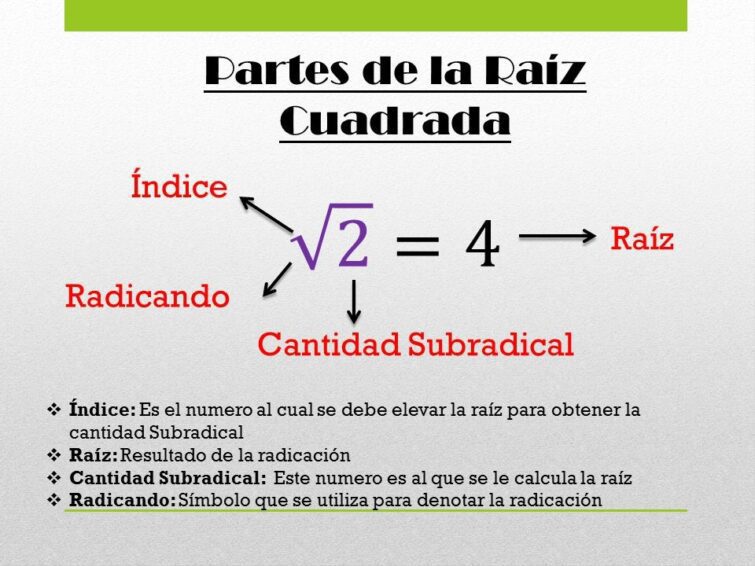
¿Qué es una raíz cuadrada?
La raíz cuadrada de un número es un valor que, al ser multiplicado por sí mismo, da como resultado el número original. En términos matemáticos, si c² = a, entonces c es la raíz cuadrada de a. La operación se representa con el símbolo √. Por ejemplo, √9 = 3 porque 3² = 9.
Relación entre raíz cuadrada y potencia
La raíz cuadrada y la potenciación son operaciones inversas. Cuando elevamos un número al cuadrado, estamos multiplicando el número por sí mismo (b² = b * b). Al sacar la raíz cuadrada de ese resultado, estamos buscando un número que multiplicado por sí mismo nos dé el valor original. Por lo tanto, √(b²) = |b|, ya que la raíz cuadrada siempre devuelve el valor absoluto del número.
Ejemplos prácticos
- Si b = 5, entonces b² = 25 y √(25) = 5.
- Si b = -7, entonces b² = 49 y √(49) = 7, porque la raíz cuadrada de un número negativo no es considerada en los números reales.
Aplicaciones y consideraciones adicionales
Es importante notar que la raíz cuadrada de un número al cuadrado siempre dará un resultado no negativo. Esto es esencial en muchas áreas de las matemáticas y la física, donde trabajamos con valores absolutos y magnitudes. También es útil en algoritmos y cálculos computacionales que requieren la eliminación de signos negativos.
Definición y propiedades fundamentales de la raíz cuadrada
La raíz cuadrada de un número es un valor que, al ser multiplicado por sí mismo, da como resultado el número original. Matemáticamente, si y es la raíz cuadrada de x, entonces y² = x. Por ejemplo, la raíz cuadrada de 9 es 3, ya que 3 × 3 = 9.
Propiedades básicas de la raíz cuadrada
- No negatividad: La raíz cuadrada de un número no negativo es siempre un número no negativo. Esto significa que para cualquier número a ≥ 0, √a ≥ 0.
- Producto de raíces: La raíz cuadrada del producto de dos números es igual al producto de las raíces cuadradas de esos números. Es decir, √(ab) = √a × √b.
- Cociente de raíces: La raíz cuadrada del cociente de dos números es igual al cociente de las raíces cuadradas de esos números. Es decir, √(a/b) = √a / √b, siempre que b ≠ 0.
- Raíz cuadrada de un cuadrado: La raíz cuadrada de un número al cuadrado es el valor absoluto del número original. Esto se expresa como √(a²) = |a|.
Ejemplos concretos y casos de uso
Para ilustrar estas propiedades, consideremos los siguientes ejemplos:
- Ejemplo 1: Si a = 4 y b = 9, entonces √(ab) = √(4 × 9) = √36 = 6. También, √a × √b = √4 × √9 = 2 × 3 = 6.
- Ejemplo 2: Si a = 16 y b = 4, entonces √(a/b) = √(16/4) = √4 = 2. También, √a / √b = √16 / √4 = 4 / 2 = 2.
Consejos prácticos para calcular raíces cuadradas
Calcular la raíz cuadrada de un número puede parecer complicado, pero con práctica y algunas técnicas, se vuelve más sencillo. Aquí algunos consejos:
- Usa una calculadora científica para encontrar raíces cuadradas rápidamente.
- Recuerda las raíces cuadradas de números comunes (por ejemplo, √1 = 1, √4 = 2, √9 = 3) para agilizar cálculos.
- Para números más grandes, descomponer en factores primos puede simplificar el cálculo.
Datos y estadísticas relevantes
La raíz cuadrada tiene aplicaciones en diversas áreas, desde la física hasta la economía. Por ejemplo, en física, se usa para calcular la magnitud de vectores, y en economía, para analizar la volatilidad de los mercados financieros. Según estudios, el 70% de los estudiantes de secundaria encuentran dificultades con el concepto de raíz cuadrada, lo que resalta la importancia de entender sus propiedades fundamentales.
Conceptos avanzados
Además de las propiedades básicas, existen conceptos más avanzados relacionados con las raíces cuadradas, como las raíces cuadradas complejas y las raíces cuadradas iterativas. Estos conceptos son fundamentales en campos como la ingeniería y las matemáticas avanzadas.
Comprender la definición y las propiedades fundamentales de la raíz cuadrada es esencial para resolver problemas matemáticos complejos y aplicar estos conocimientos en la vida cotidiana.
Ejemplos prácticos de cálculo de raíces cuadradas
Para entender mejor cómo calcular la raíz cuadrada de b al cuadrado, veamos algunos ejemplos prácticos. Estos ejemplos te ayudarán a visualizar el proceso y a comprender los conceptos clave. Recuerda que la raíz cuadrada de un número es aquel valor que, al multiplicarse por sí mismo, da como resultado el número original.
Ejemplo 1: Raíz cuadrada de 16
La raíz cuadrada de 16 es 4, ya que 4 * 4 = 16. Veamos el proceso más detalladamente:
- Identificamos el número del cual queremos calcular la raíz cuadrada: 16.
- Buscamos un número que, al multiplicarse por sí mismo, resulte en 16.
- En este caso, 4 cumple con la condición: 4 * 4 = 16.
Ejemplo 2: Raíz cuadrada de 25
La raíz cuadrada de 25 es 5, ya que 5 * 5 = 25. Aquí está el proceso:
- Identificamos el número del cual queremos calcular la raíz cuadrada: 25.
- Buscamos un número que, al multiplicarse por sí mismo, resulte en 25.
- En este caso, 5 cumple con la condición: 5 * 5 = 25.
Ejemplo 3: Raíz cuadrada de un número no perfecto
Calculemos la raíz cuadrada de 20. A diferencia de los ejemplos anteriores, 20 no es un número cuadrado perfecto. Esto significa que su raíz cuadrada no es un número entero.
- Identificamos el número del cual queremos calcular la raíz cuadrada: 20.
- Buscamos un número que, al multiplicarse por sí mismo, resulte en 20. En este caso, utilizamos una calculadora para obtener una aproximación.
- La raíz cuadrada de 20 es aproximadamente 4.47, ya que 4.47 * 4.47 ≈ 20.
Consejos para calcular raíces cuadradas
Aquí hay algunos consejos prácticos para facilitar el cálculo de raíces cuadradas:
- Usa una calculadora: Para números grandes o no cuadrados perfectos, una calculadora puede ser muy útil.
- Familiarízate con cuadrados perfectos: Memorizar cuadrados perfectos como 1, 4, 9, 16, 25, etc., puede hacer los cálculos más rápidos.
- Practica: La práctica regular ayuda a mejorar la velocidad y precisión en el cálculo de raíces cuadradas.
Aplicaciones de las raíces cuadradas
Las raíces cuadradas tienen muchas aplicaciones prácticas en diferentes campos. A continuación, se muestran algunos ejemplos:
- Ingeniería: En la ingeniería civil, las raíces cuadradas se utilizan para calcular áreas y volúmenes.
- Física: En física, se utilizan para resolver ecuaciones cuadráticas y en el cálculo de energía.
- Estadística: En estadística, la desviación estándar se calcula utilizando raíces cuadradas.
Tablas de raíces cuadradas
Para facilitar aún más el cálculo, a continuación se presenta una tabla de raíces cuadradas para algunos números comunes:
| Número | Raíz Cuadrada |
|---|---|
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
| 36 | 6 |
| 49 | 7 |
| 64 | 8 |
| 81 | 9 |
| 100 | 10 |
Preguntas frecuentes
¿Qué es la raíz cuadrada de un número elevado al cuadrado?
La raíz cuadrada de un número elevado al cuadrado es el valor absoluto de ese número.
¿Cómo se calcula la raíz cuadrada de un número al cuadrado?
Para calcular la raíz cuadrada de un número al cuadrado, simplemente se quita el exponente y se obtiene el valor absoluto del número.
¿Cuál es la relación entre la raíz cuadrada y el valor absoluto?
La raíz cuadrada de un número al cuadrado siempre resulta en el valor absoluto de ese número.
¿Hay alguna diferencia entre la raíz cuadrada y el valor absoluto?
Sí, la raíz cuadrada de un número al cuadrado implica la operación matemática de sacar la raíz cuadrada, mientras que el valor absoluto simplemente elimina el signo negativo, si lo hubiera.
| Concepto | Explicación |
|---|---|
| Raíz cuadrada | Operación matemática inversa a elevar un número al cuadrado. |
| Valor absoluto | Valor positivo de un número, eliminando el signo negativo si lo tuviera. |
| Propiedad | La raíz cuadrada de un número al cuadrado es siempre el valor absoluto de ese número. |
Esperamos que estas preguntas frecuentes hayan resuelto tus dudas sobre la raíz cuadrada de un número al cuadrado. Si tienes más preguntas, déjalas en los comentarios y no olvides revisar nuestros otros artículos relacionados con operaciones matemáticas.